通用矩阵乘（GEMM）优化算法

引言

气象预报、石油勘探、核子物理等现代科学技术大多依赖计算机的计算模拟，模拟计算的核心是表示状态转移的矩阵计算。另一方面，计算机图形处理以及近年来兴起的深度学习也和矩阵乘高度相关。而矩阵乘对计算资源消耗较大，除了计算机体系结构的不断更新外，软件优化方面也有大量的研究工作。

本文简要介绍通用矩阵乘（GEMM，General Matrix Multiplication）优化的基本概念和方法、神经网络量化中矩阵乘的优化方法。旨在帮助大家在概念中建立一些直觉，无甚高论。

通用矩阵乘概念

矩阵乘通常定义为：

$C = AB ; A,B,C \in R^{n\times n}$

$C_{m,n} = \sum_{k=1}^{K}A_{m,k}B_{k,n}; m,n,k\in R^n$

其中 $A,B,C$ 三者的形状分别为 $M\times K , K \times N , M \times N$ 。

下面图一是矩阵乘的可视化展示，和计算时为得到一个输出点所要使用的输入数据。

图一：矩阵乘一个输出元素的计算

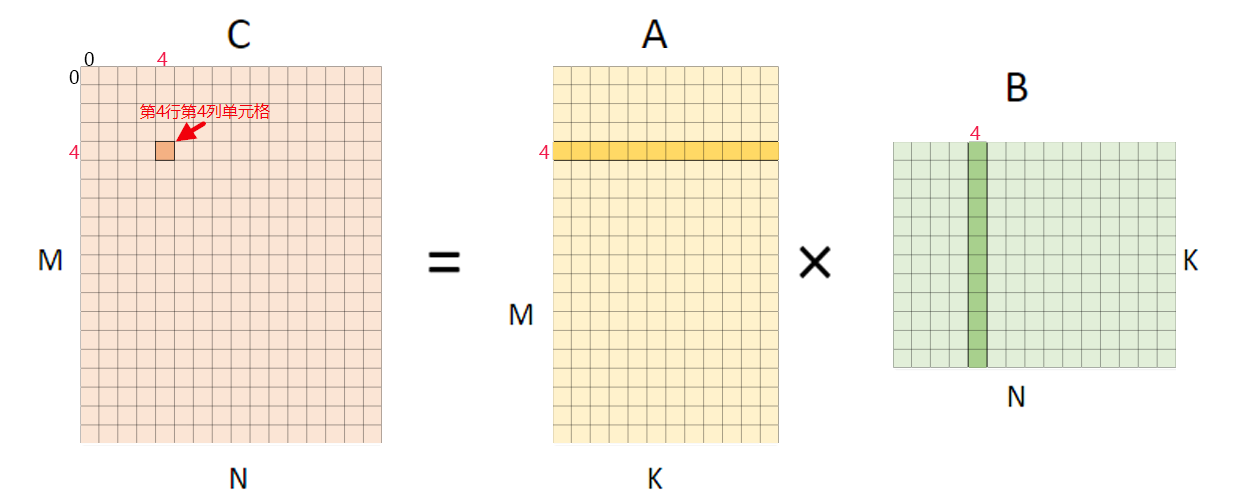
与之相对应的伪代码表示为：

for (int m = 0; m < M; m++) {
  for (int n = 0; n < N; n++) {
    C[m][n] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n] += A[m][k] * B[k][n];
    }
  }
}

对这样的矩阵乘的算法优化可分为两类：

基于算法分析的方法：根据矩阵乘计算特性，从数学角度优化，典型的算法包括 Strassen 算法和 Coppersmith–Winograd 算法。
基于软件优化的方法：根据计算机存储系统的层次结构特性，选择性地调整计算顺序，主要有循环拆分向量化、内存重排等。
下面将简要介绍几种典型的方法。

基于算法分析的方法

算法分析可知，朴素的矩阵乘算法的时间复杂度为。在很长的时间内，人们认为矩阵乘在算法层面是无法优化的，而自 Strassen 算法伊始，复杂度边界便被不断降低，如图一。目前最快的方法是 Coppersmith–Winograd 算法。

图二：矩阵乘算法复杂度边界的演变

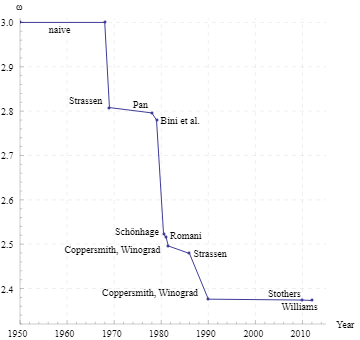
这些算法一般要求三个矩阵符合约束 $A,B,C \in R^{n^2 \times n^2}$ 。

Strassen 算法

Volker Strassen 在 1969 年提出了复杂度为 $O(n^{log_27})$ 的矩阵乘算法。这是历史上第一次将矩阵乘的计算复杂度降低到 $O(n^3)$ 以下。

基于分治（Divide and Conquer）的思想，Starssen 算法将矩阵 $A,B,C \in R^{n^2 \times n^2}$ 分别拆分为更小的矩阵

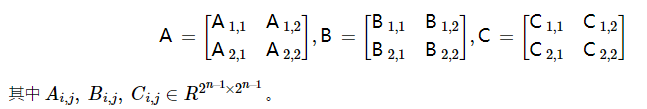
根据矩阵基本的运算法则，拆分后朴素算法的计算如下所示，共需要八次小矩阵乘法和四次小矩阵加法计算。

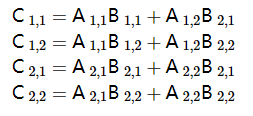
显然，分治本身并不能改进矩阵乘的计算效率。在很长的时间内，人们认为矩阵乘没有什么优化算法，直到 Strassen 引入了七个如下所示的用于辅助计算的中间矩阵

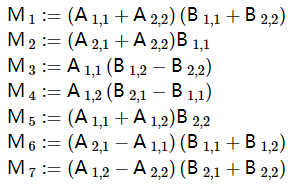
在得到这些中间矩阵的记过后，再将其组合得到最后的矩阵：

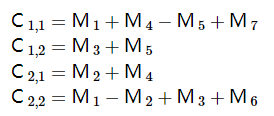
通过七次乘法和十八次加法，Strassen 算法将矩阵乘的算法复杂度降低到了 $O(n^{log_27})$ （递归地运行该算法）。如图二所示，该算法突破性地将矩阵乘计算复杂度从 $O(n^2)$ 拉了下来，后续的算法都是对该算法的某种程度上的改进。而 Strassen 算法也成为了个大算法教材讲解复杂度分析的重要示例。

完全应用 Strassen 算法的一个局限是其要求矩阵乘的规模为 $2^n$ ，这在现实情况中不容易满足。一种解决方法是将规模分解为 $2^n X$ 其中 $X$ 无法被 2 整除，那么可以应用 Strassen 算法不断递归拆分计算直到小矩阵规模为 $X$ 。此时可以用朴素算法计算小矩阵；或者将 $X$ 补零为 $2^n$ 再继续应用 Strassen 算法（亦可直接对大矩阵补零）。最终的性能取决于实现方法和运行的硬件平台。

Coppersmith–Winograd 算法

Strassen 算法提出之后，学者们不断尝试继续降低复杂度，因为 $O(n^{log_27})$ 的代价还是太高了。另一方面，Strassen 算法虽然学术意义很大，但实际应用却有限。矩阵乘算法的复杂度边界终于在 Don Coppersmith 和 Shmuel Winograd 的合作下在 1990 年突破性地降低到了 $O(n^{2.376})$ 。

Coppersmith–Winograd 算法的思想和 Strassen 算法类似。其证明过程比较复杂，使用的定理太多，这里就不再介绍（实际上是没看懂…），有兴趣的可以参考下面几篇文章：

在 Coppersmith–Winograd 算法之后，学者们依然在不断尝试降低矩阵乘算法的复杂度，但 Strassen 算法和 Coppersmith–Winograd 算法目前依然是矩阵乘算法优化的两个里程碑。

基于软件优化的方法

除了从算法分析的角度优化通用矩阵乘，在实际的计算机系统中应用很多的还有软件优化的方法。软件优化方法基于对计算机体系机构和软件系统的特征分析，结合具体计算的特性，设计出针对性的优化方法。对矩阵乘而言，比较重要的软件优化方向包括：改进访存局部性、利用向量指令等。

我们回顾一下矩阵乘的伪代码，其计算操作总数为 $2_{mla}MNK$
（其中 $M$ 、 $N$ 、 $K$ 分别指代三层循环执行的次数，2 指代循环最内层的一次乘法和加法），内存访问操作总数为 $(2 + 1 + 1)MNK = 4MNK$ （其中 $MNK$ 是累加求和的循环， $2 + 1 + 1$ 指代对 $C, A, B$ 三者的内存访问， $C$ 需要先读取内存、累加完毕再存储，且忽略对 $C$ 初始化时的操作）。GEMM 基于软件优化的性能改进以此为基点。

How to optimize gemm 介绍了如何采用各种优化方法，将最基础的计算改进了约七倍（如图三）。其基本方法是将输出划分为若干个 $4 \times 4$ 子块，以提高对输入数据的重用。同时大量使用寄存器，减少访存；向量化访存和计算；消除指针计算；重新组织内存以地址连续等。详细的可以参考原文。

图三：How to optimize gemm 的优化效果

计算拆分展示

本节主要以图形化的方式介绍计算拆分。

图四将输出的计算拆分为 $1\times4$ 的小块，即将 $N$ 维度拆分为两部分。计算该块输出时，需要使用 $A$ 矩阵的 1 行，和 $B$ 矩阵的 4 列。

图四：矩阵乘计算 $1 \times 4$ 输出

下面是该计算的伪代码表示，这里已经将 $1 \times 4$ 中 $N$ 维度的内部拆分进行了展开。这里的计算操作数仍然是 $2MNK$ ，这一点在本文中不会有变化。这里的内存访问操作数尚未出现变化，仍然是 $4MNK$ ，但接下来会逐步改进。

for (int m = 0; m < M; m++) {
  for (int n = 0; n < N; n += 4) {
    C[m][n + 0] = 0;
    C[m][n + 1] = 0;
    C[m][n + 2] = 0;
    C[m][n + 3] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n + 0] += A[m][k] * B[k][n + 0];
      C[m][n + 1] += A[m][k] * B[k][n + 1];
      C[m][n + 2] += A[m][k] * B[k][n + 2];
      C[m][n + 3] += A[m][k] * B[k][n + 3];
    }
  }
}

简单的观察即可发现，上述伪代码的最内侧计算使用的矩阵 $A$ 的元素是一致的。因此可以将 $A[m][k]$ 读取到寄存器中，从而实现 4 次数据复用（这里不再给出示例）。一般将最内侧循环称作计算核（micro kernel）。进行这样的优化后，内存访问操作数量变为 $(2 + 1+\frac{1}{4})MNK$ ，其中 $\frac{1}{4}$ 是对 $A$ 优化的效果。

类似地，我们可以继续拆分输出的 $M$ 维度，从而在内侧循环中计算 $4 \times 4$ 输出，如图五。

图五：矩阵乘计算 $4 \times 4$ 输出

同样地，将计算核心展开，可以得到下面的伪代码。这里我们将 $1 \times 4$ 中展示过的 $N$ 维度的计算简化表示。这种拆分可看成是 $4 \times 1 \times 4$ ，这样 $A$ 和 $B$ 的访存均可复用四次。由于乘数效应， $4 \times 4$ 的拆分可以将对输入数据的访存缩减到
$2MNK + \frac{1}{4}MNK + \frac{1}{4} MNK = \frac{5}{2}MNK$