前几篇的博客都是步长为1的卷积神经网络例子,现在以步长为2的例子来说明步长不为1的情况。
下面是一个7x7的灰度图像的矩阵,以及一个3x3的过滤器,卷积运算之后的输出结果应该为3x3的矩阵。
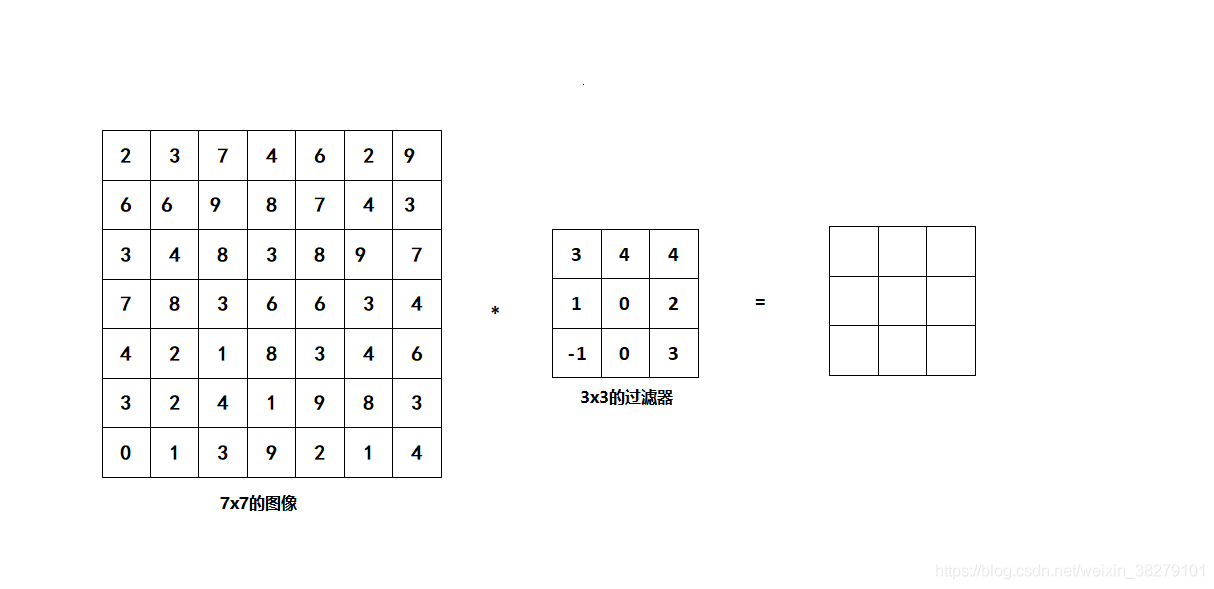
具体计算过程:
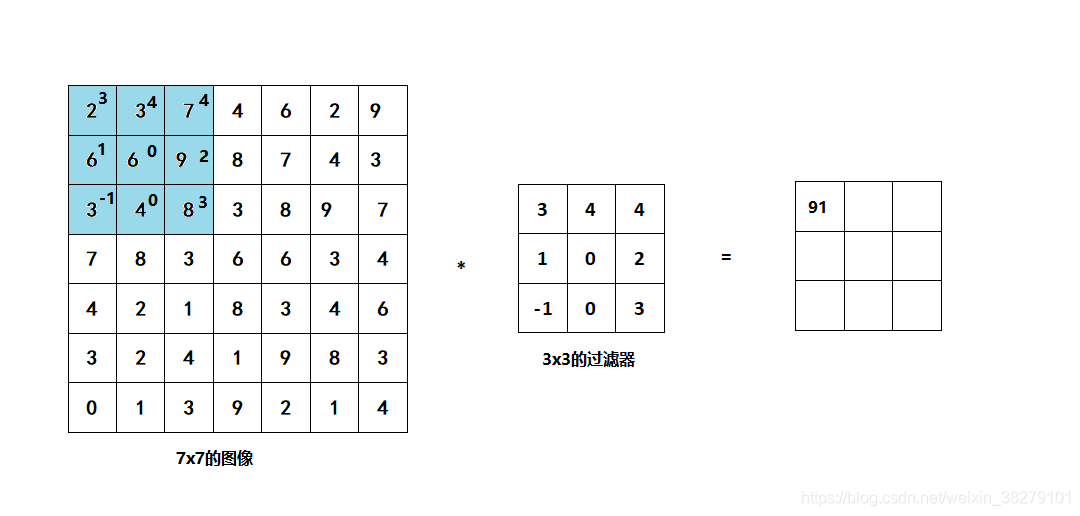
还和之前一样取左上方的3×3区域的元素的乘积,再加起来,最后结果为91。
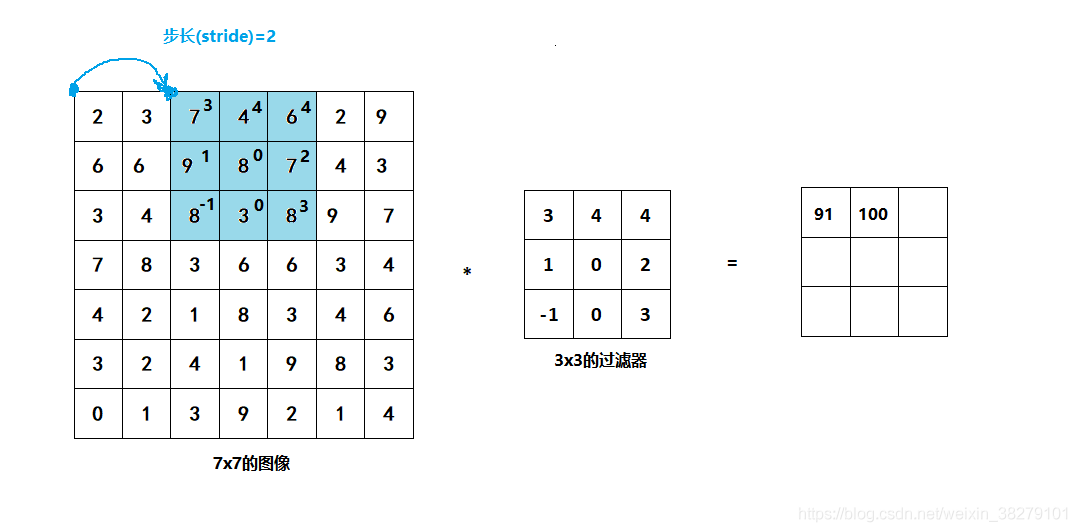
之前我们移动蓝框的步长是1,现在移动的步长是2,我们让过滤器跳过2个步长,注意一下左上角,这个点移动到其后两格的点,跳过了一个位置。然后你还是将每个元素相乘并求和,你将会得到的结果是100。
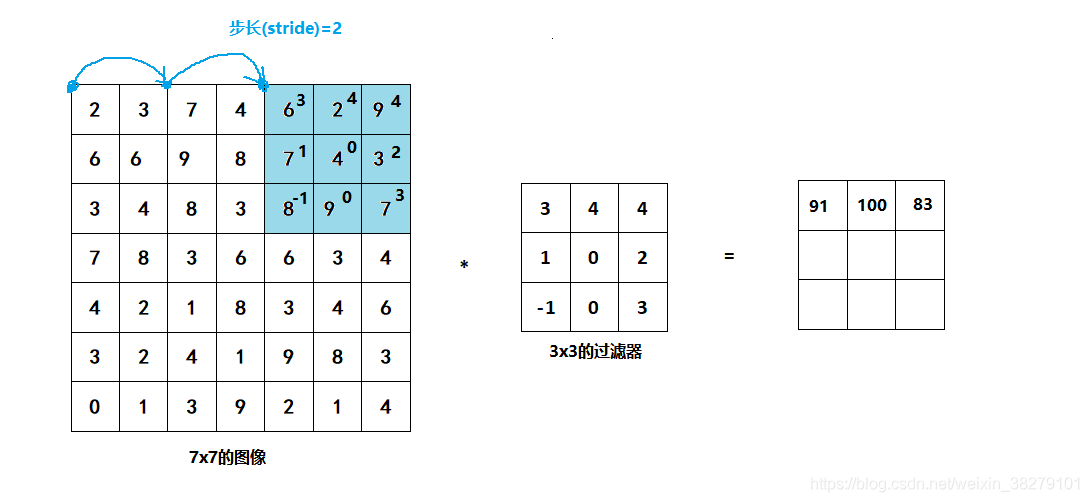
继续将蓝色框移动两个步长,你将会得到83的结果。当你移动到下一行的时候,你也是使用步长2而不是步长1,所以我们将蓝色框移动到这里:
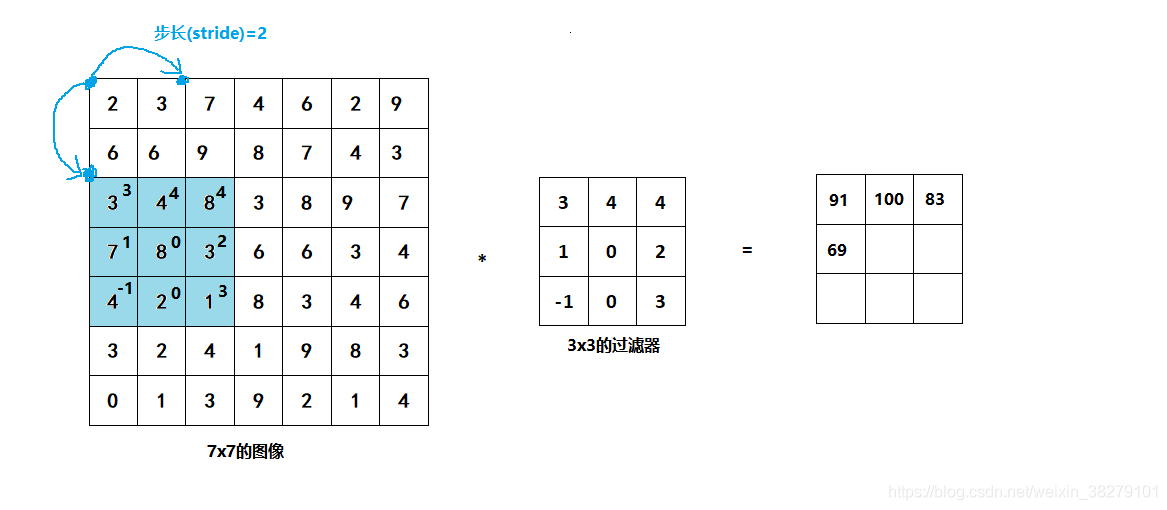
注意到我们跳过了一个位置,得到69的结果,现在你继续移动两个步长,会得到91,127,最后一行分别是44,72,74。
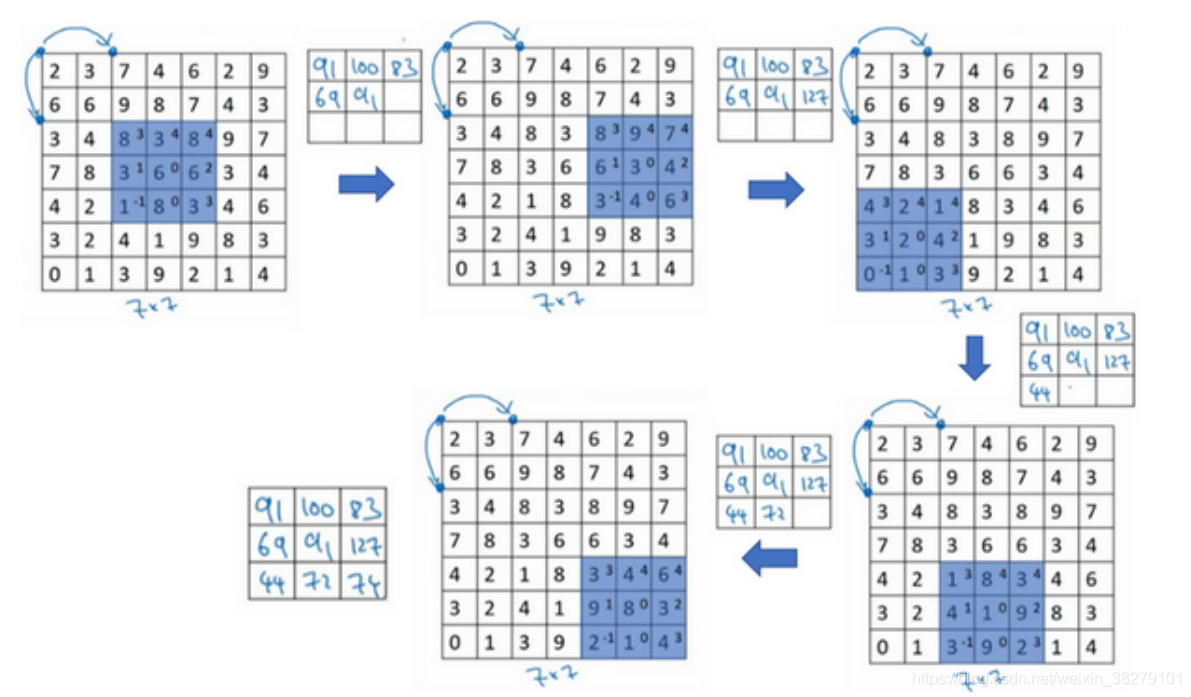
所以在这个例子中,我们用3×3的矩阵卷积一个7×7的矩阵,得到一个3×3的输出。输入和输出的维度是由下面的公式决定的。如果你用一 个f × f 的过滤器卷积一个 n × n 的图像,你的 padding 为 p ,步幅为 s ,在这个例子中 s = 2,你会得到一个输出,因为现在你不是一次移动一个步子,而是一次移动s个步子,输出于是变为 。在我们的这个例子里,n = 7 ,p = 0,f = 3,s = 2 , ,即3×3的输出。
现在只剩下最后的一个细节了,如果商不是一个整数怎么办?在这种情况下,我们向下取整。⌊ ⌋这是向下取整的符号,这也叫做对z进行地板除(floor),这意味着z向下取整到最近的整数。这个原则实现的方式是,你只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。你的3×3的过滤器必须完全处于图像中或者填充之后的图像区域内才输出相应结果,这就是惯例。因此正确计算输出维度的方法是向下取整,以免 不是整数。
总结一下维度情况,如果你有一个的矩阵或者的图像,与一个的矩阵卷积,或者说的过滤器。Padding是步幅为没输出尺寸就是这样:

可以选择所有的数使结果是整数是挺不错的,尽管一些时候,你不必这样做,只要向下取整也就可以了。
原文:
作者:谦小白
链接:https://blog.csdn.net/weixin_38279101/article/details/103820166
