本篇讨论卷积层前项传播过程中的主要计算:卷积算法的实现
卷积计算的输入从二维的矩阵到四维张量,以及卷积核从二维矩阵到四维矩阵都对应不同大小的输出,最后会统一到一个算法里面,这里用一个函数来表示:
a=conv(x,w)
x 是输入, w 是卷积核, a 是卷积的结果,即特征图(feature map)。
注:
有的人叫它为 输出特征图。
单通道:
先看看输入和卷积核都是矩阵的情况:
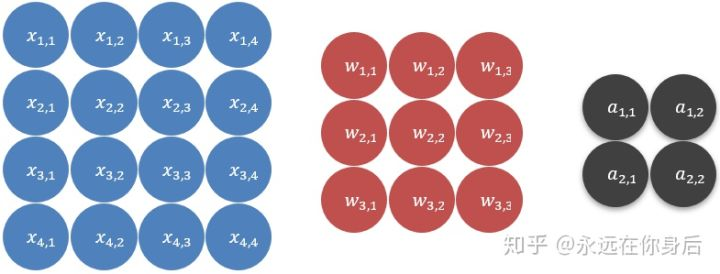
蓝色的为输入,红色的是卷积核,灰色是结果(即:输出特征图)
卷积的过程就是,将输入划分成若干个与卷积核相同大小的不同子集,这些子集再分别与卷积核点乘相加:
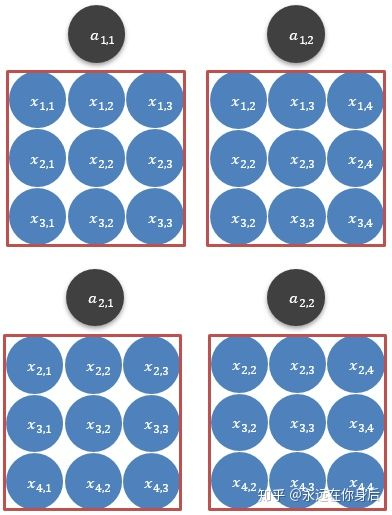
如上图所示,本例的输入可以划分为4个子集(为什么是4个,这里涉及一个步长的变量stride,后面讨论),将它们各自与卷积核点乘,得到的结果就是输出红框内容。
现在,将上述的过程用公式向量表示,就拿第一个子集矩阵(将其表示为 x(1))来说吧:
x(1)=⎣⎡x1,1x2,1x3,1x1,2x2,2x3,2x1,3x2,3x3,3⎦⎤
然后将其矩阵按行展开,变成一个行向量:
x(1)=[x1,1x1,2x1,3x2,1x2,2x2,3x3,1x3,2x3,3]
对这四个子集x(1)x(2)x(3)x(4)都进行同样的操作,然后并在一起得到一个矩阵:
X=⎣⎢⎢⎡x(1)x(2)x(3)x(4)⎦⎥⎥⎤
同样的,再将卷积核如法炮制,只不过这次是展开成列向量:
W=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡w1,1w1,2w1,3w2,1w2,2w2,3w3,1w3,2w3,3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
但是有人为了节省纸张,将其写成横向转置的形式:
W=[w1,1w1,2w1,3w2,1
热点文章:


