比特币的所有权是通过数字密钥、比特币地址和数字签名来确定的。数字密钥实际上并不存储在网络中,而是由用户生成之后,存储在一个叫做钱包的文件或简单的数据库中。用户钱包中的数字密钥完全独立于比特币协议,可由用户的钱包软件生成并管理,而无需参照区块链或访问互联网。密钥实现了比特币的许多有趣特性,包括去中心化信任和控制、所有权认证和基于密码学证明的安全模型。
大多数比特币交易都需要在区块链中存储一个有效的数字签名。该数字签名只能由密钥产生,因此拥有密钥副本就等于拥有了该帐户中比特币的控制权。用于支出资金的数字签名也称为见证(witness),这是加密技术中的术语。 比特币交易中的见证数据证明了资金的真正所有权。
密钥是成对出现的,由私钥和公钥所组成。公钥就像银行的帐号,而私钥就像PIN码或支票的签名。比特币的用户很少会直接看到数字密钥。一般情况下,它们存储在钱包文件内,由比特币钱包软件进行管理。
在比特币交易的支付环节,收款人的公钥由数字指纹表示,称为比特币地址,就像支票上收款人名称 (即“付给谁的账户”)。一般情况下,比特币地址由公钥生成并与之对应。然而,并非所有比特币地址都代表公钥; 也可以代表其他支付对象,譬如脚本,我们将在本章后面提及。这样一来,比特币地址就可以抽象成资金接收者,使得交易更灵活,就像纸质支票:可以支付到个人账户、公司账户,支付账单和现金。比特币地址是密钥的唯一形式,人们只需要把比特币地址告诉别人就可以。
首先,我们将介绍密码学,并解释在比特币中使用的数学知识。然后我们将了解密钥的产生、存储和管理方式。我们将检查私钥和公钥、地址和脚本地址的各种编码格式。最后,我们将讲解密钥和地址的高级用途:比特币靓号地址,多重签名以及脚本地址和纸钱包。
4.1.1 公钥加密和加密货币
公钥加密发明于20世纪70年代,它是计算机和信息安全的数学基础。
公钥加密被发明之后,一些合适的数学函数被发现,譬如:素数幂运算和椭圆曲线乘法。这些数学函数都是不可逆的, 就是说很容易向一个方向计算,但不可以向相反方向倒推。基于这些数学函数的密码学,使得生成数字密钥和不可伪造的数字签名成为可能。比特币正是使用椭圆曲线乘法作为其公钥加密的基础。
在比特币系统中,我们用公钥加密创建一个密钥对,用于控制对比特币的访问。密钥对包括一个私钥,和由其衍生出的唯一的公钥。公钥用于接收比特币,而私钥用于支付时进行交易签名。
公钥和私钥之间的数学关系,使得私钥可用于生成特定消息的签名。公钥则可以在不显示私钥的情况下验证签名。
支付比特币时,比特币的当前所有者需要在交易中提交其公钥和签名(每次交易的签名都不同,但都由同一个私钥生成)。针对展示的公钥和签名,比特币网络中的所有人都可以验证该交易有效并予以接受,从而确认支付者对该交易中的比特币的所有权。
提示 大多数比特币钱包工为了方便会将私钥和公钥以密钥对的形式存储在一起。然而,公钥可以由私钥计算得到, 所以只存储私钥也是可以的。
4.1.2 私钥和公钥
一个比特币钱包中包含一系列的密钥对,每个密钥对包括一个私钥和一个公钥。私钥(k)是一个数字,通常是随机选出的。基于私钥,我们就可以使用椭圆曲线乘法这个单向加密函数产生一个公钥(K)。基于公钥(K),我们就可以使用一个单向加密哈希函数生成比特币地址(A)。在本节中,我们将从生成私钥开始,讲述如何使用椭圆曲线运算将私钥生成公钥,并最终由公钥生成比特币地址。私钥、公钥和比特币地址之间的关系如下图所示。
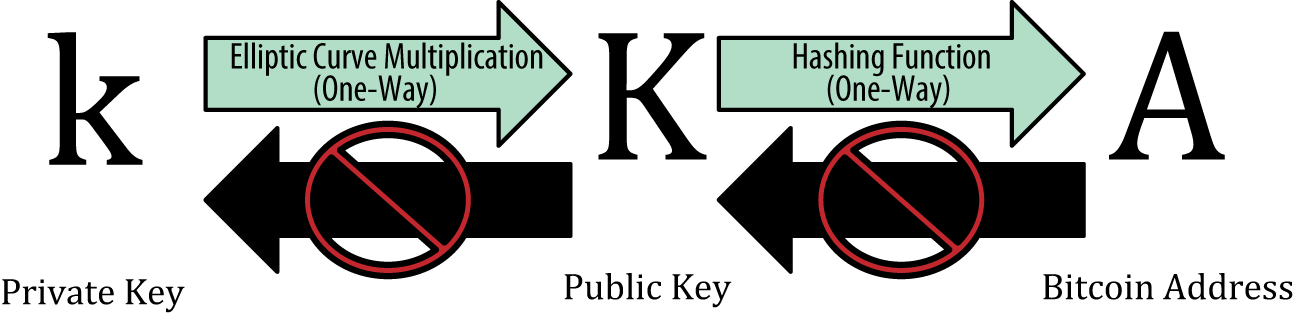
图4-1:私钥、公钥和比特币地址之间的关系
为什么使用非对称加密(公钥/私钥)?
为什么在比特币中使用非对称加密技术? 它不是用于对交易进行“加密”(保密)的。 相反,非对称加密技术的最有用特性是生成数字签名。 可以将私钥用作交易的数字指纹来产生数字签名。 该签名只能由知晓私钥的人生成。 但是,任何访问公钥和交易指纹的人都可以验证签名。 这种非对称密码学的适用性使得任何人都可以验证每笔交易的每个签名,并且确保只有私钥的所有者可以生成有效的签名。
4.1.3 私钥
私钥就是一个随机选出的数字而已。拥有和控制了私钥,就相当于控制了该私钥对应的比特币地址中的所有资金。通过证明比特币交易中资金的所有权,私钥可以生成花费该笔资金的签名。私钥任何情况下都必须保密,因为一旦被泄露给第三方,相当于该私钥保护之下的比特币也拱手相让了。私钥还必须进行备份,以防意外丢失,因为私钥一旦丢失就无法恢复,其所保护的比特币也将永远丢失。
提示:
比特币私钥只是一个数字。你可以用硬币、铅笔和纸来随机生成你的私钥:掷硬币256次,用纸和笔记录正反面并转换为0和1,随机得到的256位二进制数字可作为比特币钱包的私钥。该私钥可进一步生成公钥。
从一个随机数生成私钥生成密钥的第一步也是最重要的一步,是要找到足够安全的熵源,即随机性来源。生成一个比特币私钥在本质上与“在1到2256之间选一个数字”无异。只要选取的结果是不可预测或不可重复的,那么选取数字的具体方法并不重要。比特币软件使用操作系统底层的随机数生成器来产生256位的熵(随机性)。通常情况下,操作系统随机数生成器由人工的随机源进行初始化,这就是为什么也可能需要不停晃动鼠标几秒钟。
更准确地说,私钥可以是1和n-1之间的任何数字,其中n是一个常数(n=1.158 * 1077,略小于2256),并被定义为由比特币所使用的椭圆曲线的阶(见下面的椭圆曲线密码学解释这一节)。要生成这样的一个私钥,我们随机选择一个256位的数字,并检查它是否小于n-1。从编程的角度来看,一般是通过在一个密码学安全的随机源中取出一长串随机字节,对其使用SHA256哈希算法进行运算,这样就可以方便地产生一个256位的数字。如果运算结果小于n,我们就有了一个合适的私钥。否则,我们就用另一个随机数再重复一次。
警告:
不要自己写代码来生成随机数,也不要使用编程语言提供的简易随机数生成器来获得一个随机数。使用密码学安全的伪随机数生成器(CSPRNG),并且需要有一个熵源值足够的的种子。使用随机数发生器的程序库时,需仔细研读其文档,以确保它是密码学安全的。正确实施CSPRNG是密钥安全性的关键所在。
以下是一个随机生成的私钥(k),以十六进制格式表示(256位的二进制数,转变为十六进制是64位,每个十六进制数占4位):
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
提示:
比特币私钥空间的大小是2256,这是一个非常大的数字。用十进制表示的话,大约是1077,而可见宇宙被估计只含有1080个原子。
要使用Bitcoin Core客户端生成一个新的密钥(参见第三章内容),可使用 getnewaddress 命令。出于安全考虑,命令运行后只显示生成的公钥,而不显示私钥。如果要bitcoind显示私钥,可以使用 dumpprivkey 命令。 dumpprivkey 命令会把私钥以 Base58校验和编码格式显示,这种私钥格式被称为钱包导入格式(WIF,Wallet Import Format),在“私钥的格式”一节有详细讲解。下面给出了使用这两个命令生成和显示私钥的例子:
$ bitcoin-cli getnewaddress
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
$ bitcoin-cli dumpprivkey 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJdumpprivkey 命令打开钱包提取由 getnewaddress 命令生成的私钥。除非密钥对都存储在钱包里,否则bitcoind并不能从公钥得知私钥。
提示 dumpprivkey命令无法从公钥生成私钥,因为这是不可能的。这个命令只是显示钱包中已有也就是由getnewaddress命令生成的私钥。
还可以使用Bitcoin Explorer命令行工具(请参阅附录中的[appdx_bx])使用命令seed,ec-new和ec-to-wif生成和显示私钥:
$ bx seed | bx ec-new | bx ec-to-wif
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn4.1.4 公钥
通过椭圆曲线乘法可以从私钥计算得到公钥,这是不可逆转的过程:
K = kG其中:
k 是私钥;
G 是被称为生成点的常数点;
K 是所得公钥;
其反向运算,被称为“寻找离散对数”——已知公钥K来求出私钥k——是非常困难的,就像去尝试所有可能的k*值,即暴力搜索。
在演示如何从私钥生成公钥之前,我们先稍微详细学习下椭圆曲线加密算法。
提示:
椭圆曲线乘法是密码学家称之为“陷阱门”的一种函数:在一个方向(乘法)很容易计算,而在相反的方向(除法)是不可能计算出来的。 私钥的所有者可以容易地创建公钥,然后与世界共享,知道没有人可以从公钥反转该函数计算出私钥。 这个数学技巧成为证明比特币资金所有权不可伪造和安全的数字签名的基础。
4.1.5 椭圆曲线加密(Elliptic Curve Cryptography)解释
椭圆曲线加密算法是一种基于离散对数问题的非对称或者公钥加密算法,可以用对椭圆曲线上的点进行加法或乘法运算来表达。
下图是一个椭圆曲线的示例,类似于比特币所用的曲线。

图4-2椭圆曲线的示例
比特币使用了secp256k1标准所定义的一种特殊的椭圆曲线和一系列数学常数。该标准由美国国家标准与技术研究院 (NIST)建立。secp256k1曲线由下述函数定义,该函数可产生一条椭圆曲线:

上述 mod p(素数p取模)表明该曲线是在素数阶p的有限域内,也写作 Fp,其中: p = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1, 这是个非常大的素数。
因为这条曲线被定义在一个素数阶的有限域内,而不是定义在实数范围,它的函数图像看起来像二维的离散的点,因此很难可视化。不过,该公式与实数的椭圆曲线数学公式是相似的。为了举例,下图显示了在一个小了很多的素数阶17的有限域内的椭圆曲线,其形式为网格上的一系列散点。而secp256k1的比特币椭圆曲线可以被想象成一个更大的网格上一系列更为复杂的散点。
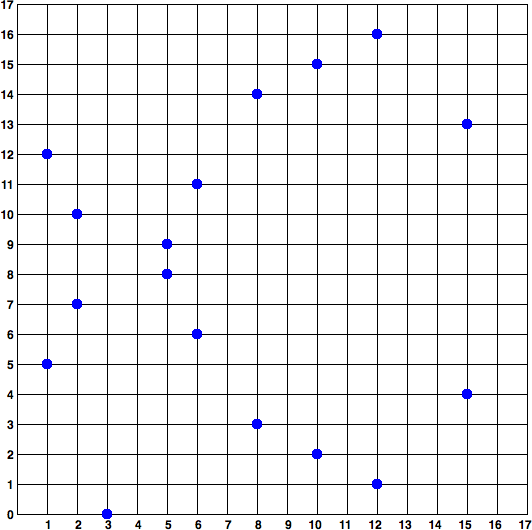
图4-3:椭圆曲线密码学F(p)上的椭圆曲线,其中p = 17
比如,下面是 secp256k1 曲线上的点P,其坐标为(x,y)。
P = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424)下面的例1显示了如何使用Python对其检验:
例1:使用pyhton确认这个点在椭圆曲线上
Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
>>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
>>> (x ** 3 + 7 - y**2) % p
0在椭圆曲线数学中,有一个点被称为“无穷远点”,这大致相当于0的作用。计算机中,它有时表示为X = Y = 0(虽然这不满足椭圆曲线方程,但这是一个可以单独检查的例子)。
还有一个 + 运算符,被称为“加法”,就像小学数学中的实数相加。给定椭圆曲线上的两个点P1和P2,则椭圆曲线上必定有第三点 P3 = P1 + P2。
从几何学上说,该第三点P3可以在P1和P2之间画一条线来计算出来的。这条直线恰好与椭圆曲线相交于另外一个地方。此点记为 P3‘= (x,y)。然后,基于x轴的对称点就是 P3=(x,-y)。
下面是几个解释为何需要“无穷远点”的特殊例子。
若 P1和 P2是同一点,那么P1和P2之间的连线延长就会与曲线相切于p1处。该切线将会与曲线相交于一个新的点。该切线的斜率可用微积分求得。尽管我们只局限在曲线上两个整数坐标的那个点,但这个机制是没问题的。
在某些情况下(即,如果P1和P2具有相同的x值,不同的y值),则切线会完全垂直,在这种情况下,P3 = “无穷远点”。
若P1就是“无穷远点”,那么其和 P1 + P2= P2。类似地,当P2是无穷远点,则P1+ P2 = P1。这表明无穷远点类似于0的角色。
事实证明,在这里 + 运算符遵守结合律,即(A+B)+C = A+(B+C)。这就是说我们可以书写成 A + B + C,不加括号也可以,而不至于混淆。
至此,我们已经定义了椭圆加法,我们可以用标准方法对加法进行扩展,来定义乘法。给定椭圆曲线上的点P,如果k是整数,则 kP = P + P + P + …+ P(k次)。注意,在这种情况下k有时被混淆了称为“指数”。
4.1.6 生成公钥
以一个随机生成的私钥k为起点,将其乘以曲线上一个预定的点,叫做生成点G得到曲线上的另一点,这就是相应的公钥 K。生成点是secp256k1标准的一部分,比特币密钥的生成点都是相同的:
{K = k * G}其中k是私钥,G是生成点,在该曲线上所得的点K是公钥。因为所有比特币用户的生成点是相同的,一个私钥k乘以G将得到相同的公钥K。k和K之间的关系是固定的,但只能单向运算,即从k得到K。这就是可以把比特币地址(K的衍生) 与任何人共享而不会泄露私钥(k)的原因。
提示 因为其中的数学运算是单向的,所以私钥可以转换为公钥,但公钥不能转换回私钥。
实现了椭圆曲线乘法,我们用之前产生的私钥k和与生成点G相乘得到公钥K:
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G公钥K 被定义为一个点 K = (x, y):
K = (x, y)其中,
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
为了可视化展示整数与点的乘积,我们使用实数范围的简化的椭圆曲线。请记住,其中的数学原理是相同的。我们的目标是找到生成点G的倍数kG。也就是将G相加k次。在椭圆曲线中,点的相加等于该点的切线与曲线相交的那个点,该点基于x轴的对称点。
下图显示了在曲线上得到 G、2G、4G 的几何做法。
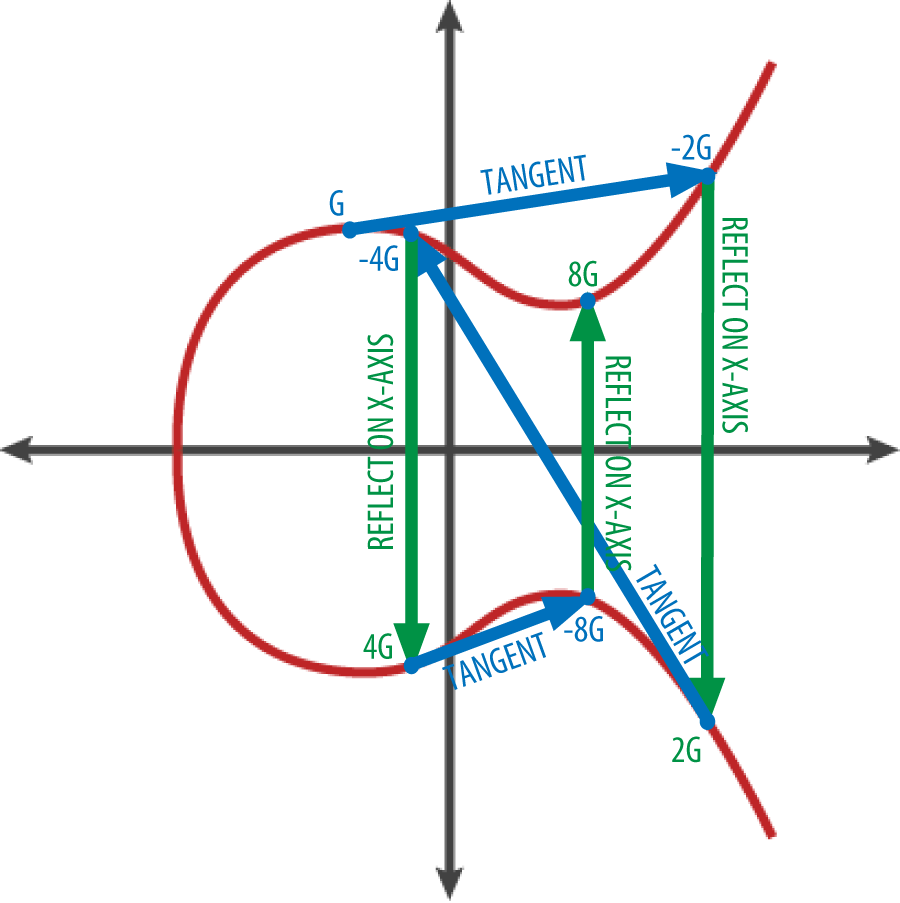
图4-4曲线上 G、2G、4G 的几何做法
提示大多数比特币程序使用OpenSSL加密库进行椭圆曲线计算。例如,调用EC_POINT_mul() 函数,可计算得到公钥。
