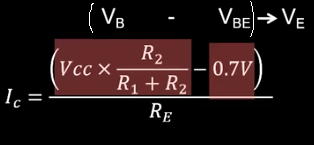由 电阻 构成的 恒流源
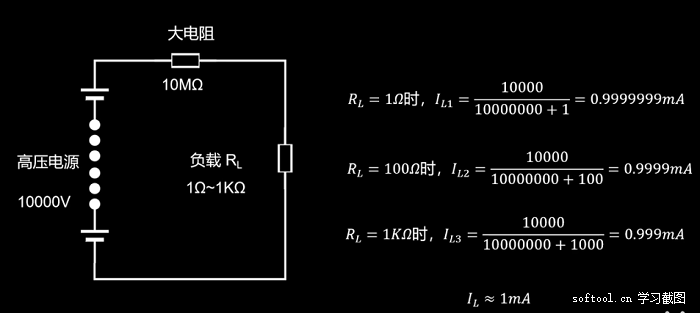
缺点:
- 高压电源 不常用
- 大电阻 会引起功耗大
- 灵活性差(如果想得到不同的供电电流,需要不停的更换大电阻)
1个 三极管
简单 三极管 恒流源
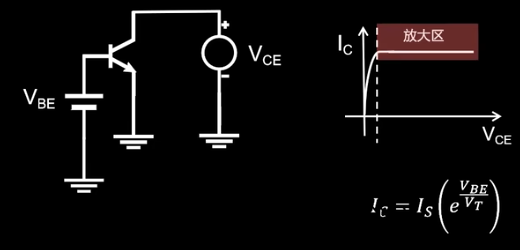
让三极管工作在放大区时,在给定的Ube下,其输出的电流Ic是恒定的(即 不随Uce变化)。
Ic=Is(eUtUbe)
最简单的情况,我们可以先用 两个电阻分压电路给三极管提供一个偏置电压Ube,然后在三极管集电极和Vcc之间接一个负载Rload,那么此时流过负载的电阻也遵循上面的公式:
Ic=Is(eUtUbe)
也就是: Ic由电阻分压产生的Ube决定。
缺点:
受 电阻精度、温度、电源纹波 的影响 导致该电路精度很差。
此时可以在 三极管的发射极 串联一个 Re ,目的是 提高恒流源的输出电阻,且降低输出电流对温度的敏感性。
输出电流由下面公式决定:
Ic=ReVcc×R1+R2R2−0.7v
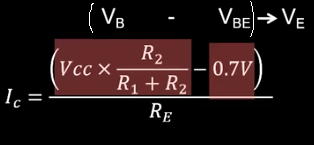
ReUe=Ie≈Ic
改进
为了减小 Vcc 电源纹波的影响,可以将 R2 用一个 稳压二极管 代替,从而提供一个稳定的基极电压。
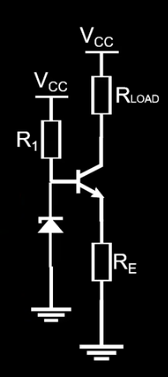
此时输出电流由公式决定:
Ic=ReUdz−0.7v
- $$U_{dz}$$ 为 稳压二极管两端的电压
- 0.7v 是 三极管的结压降Ube
2个三极管
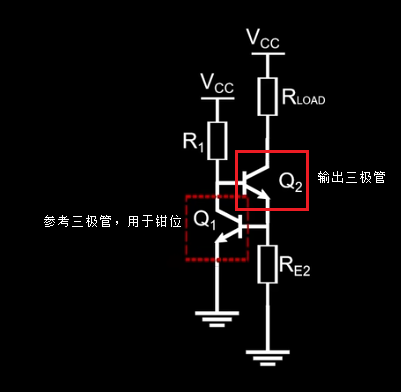
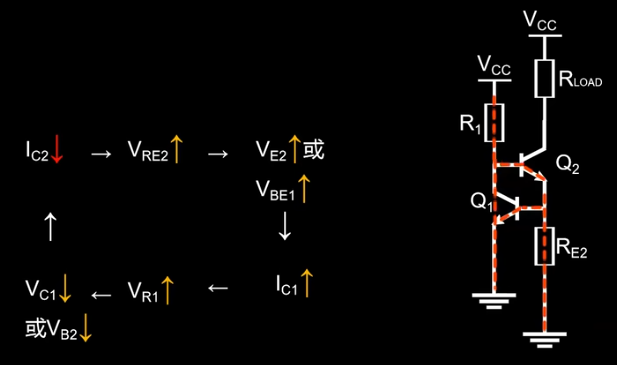
上图负反馈的过程:
上电启动时,Vcc给Q2提供基极电流,使Q2导通, Ic2增大, Ure2增加, Ue2增加或Ue1增加,驱动Q1基极,使Q1导通,即Ic1增大,导致 R1的压降增大,则Q1的集电极电压Vc1减小,从而减小了Ic2,形成闭环负反馈机制。
3:14
流过 Re2 的电流:
Ie2=Re2Ube1≈Re20.7v
那么负载Rload的电流推导:
Ic2≈Ie2≈Re20.7v
从而可以知道:
只要调节Re2的大小即可得到想要的负载电流。
缺点:
改进1:
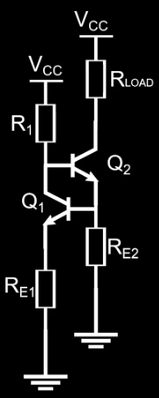
在 Q1 的发射极接一个对地电阻 Re1 ,目的是增加该恒流源的输出阻抗,减小对温度的敏感性,稳定性和精确性有明显提升,此时的输出电流公式为:
Ic2=Re2(R1+Re1)Re1(Vcc−Ube)+R1Ube
改进2:
相对上面而言
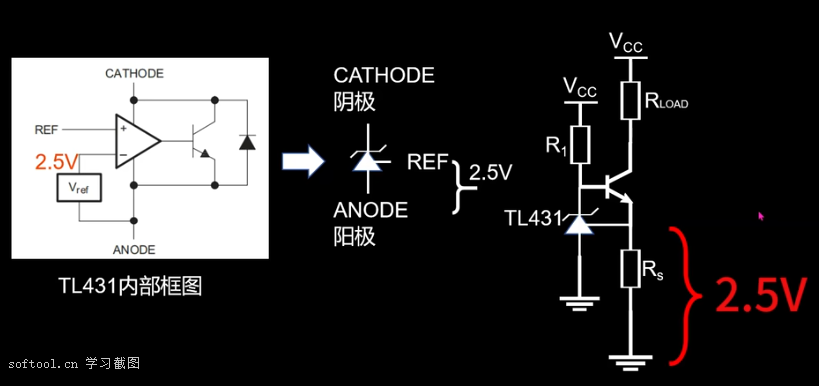
该电路依赖于 TL431 这个稳压基准芯片。
IL=RsUref=Rs2.5v
由该式可知,只需选择不同的Rs,即可得到不同的电流。
缺点:
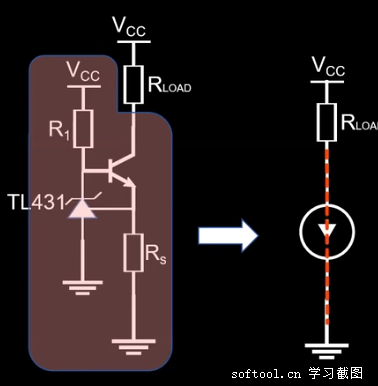
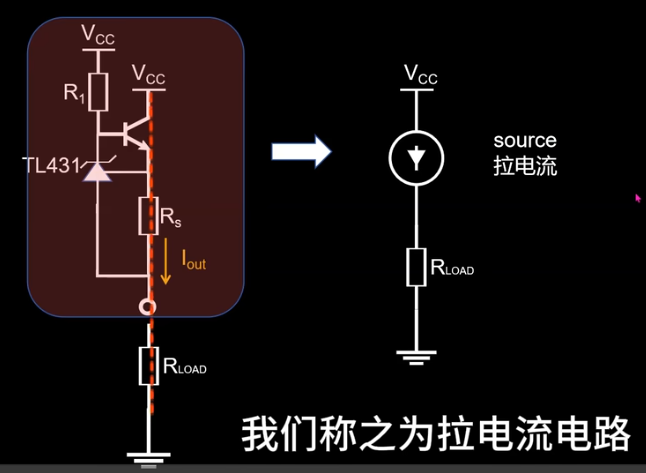
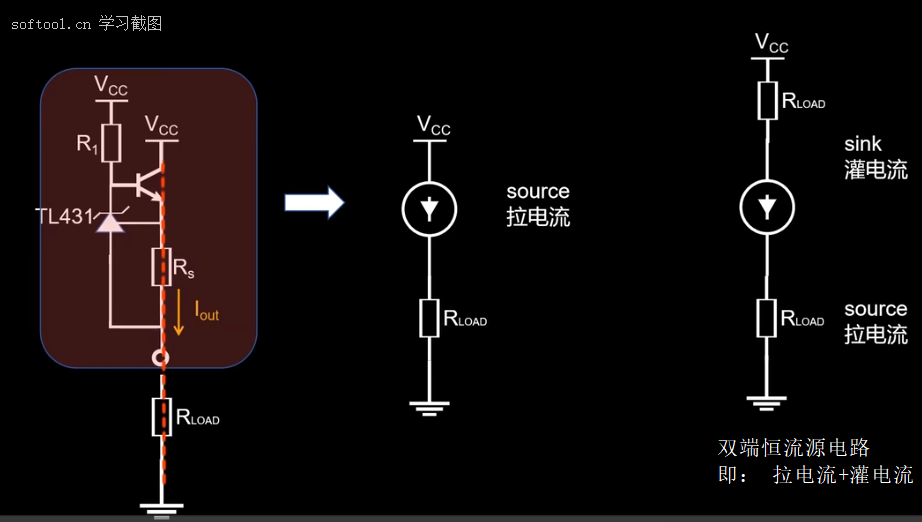
笔记:
上面的几种电路,现实中并不会用,因为精度不高。
来源:
https://www.bilibili.com/video/BV1B5v1BVEGb